COMP 2014J LEARNING PROCESS

本文最后更新于：2024年10月25日 下午

Lecture 0

Lecture: David Lillis

2 Assignment (40%) and Written Final Exam(60%)

Lecture 1

Tree

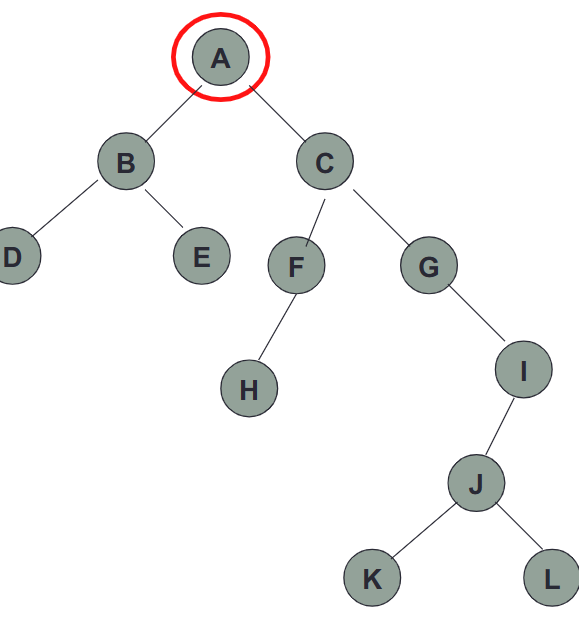
树是按层构造的数据结构，每个数据间的关系是父与子。-

  • 数据储存在Node中
  • 每个节点有且仅有一个父节点（除root节点），可以有任意数量的子节点。

术语

  • Root of tree: A 头节点，没有父节点

  • Parent of H: F

  • Children of J : K, L

  • Siblings of F: G 姊妹节点

  • Internal Nodes: A, B, C, F, G, I, J (至少有一个子节点)

  • External Nodes: D, E, H, K, L (没有子节点)

  • Ancestor of I: A, C, G, I (自己也可以是自己的祖先)

  • Descendant of I: I, J, K, L (自己也是自己的后代)

  • Edge: (U,V) U 是 V 的父节点

    （A, B), (G, I), BUT (A, G), (F, C) 不是Edge.

  • Path: 从上到下的有序路径

    （A, C, G, I)

  • Depth of a node: 该节点祖先的个数，不包括该节点。Depth(A) = 0 Depth(G) = 2

  • Degree of a node: 该节点子节点的个数。degree(A) = 2, degree(G) = 1

  • Height of a tree： 树的层数 height(T) = 5. 最高的节点高度就是树的层数.

  • Subtree of tree T rooted at node v : 子树

image-20240307215642213

二叉树

最多允许有两个子节点，分为左子节点和右子节点，左节点在右节点之前。

真二叉树(Proper Binary Tree): 节点的度为0或2

  • 通过将外部节点扩展为内部节点来实现树

  • 只有内部节点存储数据，外部节点为空

  • 关键操作

    • expandExternal(p, e) 创建两个新的空位置,并将它们作为p的左右子元素添加，并将元素e存储在p处。如果p不是外部的，则会发生错误。
    • remove(p) 如果p的左子元素是外部的，则删除它和p并用右子元素替换p。如果右子节点是外部的，删除它和p并用左子节点替换它。如果两个子节点都在内部或p在外部，则会出错。

    如果一个节点的两个子节点都是内部节点，则无法删除。朴素的理解，删除后无法确定两个姊妹节点的关系。

练习

Lecture 2 Tree Traversals and Binary Search Trees

树的遍历和访问者模式

先序遍历：中，左，右 遍历后对于任意的节点都应满足这个顺序

image-20240308113222487

实现：

1
2
3
4
5
6
7
8
9
// 递归实现
void preorder(TreeNode root) {
    if(root == null) {
        return;
    }
    print(root.val);
    preorder(root.left);
    preoerder(root.right);
}

中序遍历：左，中，右 只对二叉树有意义

image-20240308114134154

实现：

1
2
3
4
5
6
7
8
9
// 递归实现
void inorder(TreeNode root) {
    if(root == null) {
        return;
    }
    preorder(root.left);
    print(root.val);
    preoerder(root.right);
}

后序遍历：左，右，中

image-20240308114417818

实现：

1
2
3
4
5
6
7
8
9
// 递归实现
void postorder(TreeNode root) {
    if(root == null) {
        return;
    }
    preorder(root.left);
    preoerder(root.right);
    print(root.val);
}

遍历顺序的选择：

  • 释放树种的内存（一次删除一个节点）

    后序遍历：不会在删除子节点前删除他的父节点

  • 复制整个树

    前序遍历：先添加父节点的副本再添加子节点副本

  • 使用树表示文件系统结构，计算目录/文件的大小

    后序遍历：先计算子树大小，相加得到目录大小

  • 二叉搜索树中的排序

    中序遍历

思考题：
利用先序与中序遍历构造二叉树

测试链接LeetCode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static TreeNode buildTree(int[] pre, int[] in) {
		if (pre == null || in == null || pre.length != in.length) {
			return null;
		}
		HashMap<Integer, Integer> map = new HashMap<>();
		for (int i = 0; i < in.length; i++) {
			map.put(in[i], i);
		}
		return f(pre, 0, pre.length - 1, in, 0, in.length - 1, map);
	}

	public static TreeNode f(int[] pre, int l1, int r1, int[] in, int l2, int r2, HashMap<Integer, Integer> map) {
		if (l1 > r1) {
			return null;
		}
		TreeNode head = new TreeNode(pre[l1]);
		if (l1 == r1) {
			return head;
		}
		int k = map.get(pre[l1]);
		// pre : l1(........)[.......r1]
		// in  : (l2......)k[........r2]
		// (...)是左树对应，[...]是右树的对应
		head.left = f(pre, l1 + 1, (l1 + 1) + (k - l2 - 1), in, l2, k-1, map);
        head.right = f(pre, l1 + k - l2 + 1, r1, in, k + 1, r2,map);
		return head;
	}

二叉搜索树

将元素储存为有序结构的二叉树

  1. 内部节点储存element
  2. 左子节点小于父节点
  3. 右子节点大于父节点

image-20240308121151399

中序遍历可得到正确的顺序

三种基本操作：

  • put(k, v). 加入键和值。如果k已经存在，将值替换为v.

    利用find()方法查找k，若不存在k，在find()返回的节点处(一个外部节点)扩展两个节点，将其变为内部节点，在这一节点插入(k,v). 如果存在k，则直接将v替换.

  • get(k). 返回这个键关联的值.

  • remove(k). 删除k这个键

    利用find()找到k，若k只有一个外部子节点，直接使用删除方法。如果由两个内部子节点，找到该节点的下一最大节点，将其复制到k这一节点处。

    image-20240308130244406

这三种操作基于find(k, n) 从n开始查找，如果k存在，则返回包含k的节点。如果k不存在，则返回搜索结束的外部节点。

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode find(k,n) {
    if(T.isExternal(n)) {
        return n;
    }
    if k < n.key(){
        return find(k, n.left);
    } else if(k > n.key()) {
        return find(k, n.right);
    } else {
        return n;
    }
}

性能：

空间：O(n)

时间：

  • 查找操作：在平均情况下，查找操作的时间复杂度为 O(log n)，因为每次查找都可以排除一半的节点。但如果树的结构不平衡，最坏情况下可能达到 O(n)。
  • 插入操作：插入操作的时间复杂度与查找类似，也是 O(log n)。但如果插入的数据是有序的，树会退化成链表，插入操作的时间复杂度会变为 O(n)。
  • 删除操作：删除操作的时间复杂度也与查找类似，平均情况下为 O(log n)。但同样，如果树的结构不平衡，最坏情况下可能达到 O(n)。

Example:

Lecture 3

AVL Trees 平衡二叉树

AVL：一种平衡二叉搜索树

  1. 对于任意子节点，其子树的高度相差最多为1

  2. 对于任意子节点，其子树也为AVL

  3. AVL的性能均为O(logN)

    image-20240311090328888

AVL插入：

和普通的二叉搜索树相同，但在插入后，需要检查是否仍然满足性质，若不满足，需通过trinode restructuring来维持树平衡。

  • 检查平衡：从新展开的节点开始向上搜索，比较每个节点子节点的高度，如果高度差大于1，则树不平衡。

    image-20240314203954911

插入54之后，上图树不平衡。我们从54向上搜素，找到第一个不平衡的节点Z，然后设Z的子节点（高度更高的）为Y节点，然后将Y的子节点（高度更高的）设为X。执行restructure(x)对树重建。

Trinode 重组

设(a, b, c) 为 x, y, z 按从小到大顺序排列。执行旋转操作，另B成为中间的节点(即其他两个节点的父节点)

image-20240314205130971

单次旋转：

image-20240314205211943

双次旋转：

image-20240314205531895

删除节点

被删除地节点节点成为空的外部节点。从根节点开始向下检查平衡。执行Trinode重组。

Lecture 4a Amortised-Analysis

摊销分析：考虑一系列操作的总体影响平衡每个操作的成本。

Lecture 4b Splay Trees

一种使用平摊的二叉搜索树。使用Splaying维持平衡 (move-to-root)

特殊的性质：

  • 最近访问过的节点可以再次快速访问
  • 用于数据压缩

Splaying

给定内部节点X。不断重构将X移动至根节点。根据父节点(Y)和祖父节点(Z)决定如何重构。

重构操作：

  • Zig(没有祖父节点)
image-20240416220405617

  • Zig-Zig(同AVL单旋转的形状) image-20240416220448849

    1. X替换Z，Y成为X的子节点，Z成为Y的子节点
    2. 维持树的大小关系（左小右大）
    3. 起始状态与AVL相同，结果并不同

  • Zig-Zag(同AVL双旋转的形状)

    image-20240416220941337
    1. X成为根节点，Y，Z分别是X的左右子节点
    2. 树的in-order关系维持（左小右大）
    3. 同AVL的双旋转

Splay Trees

  • get(k): 如果找到K，Splay(k)。若K不存在，对最后的外部节点的父节点执行Splay
  • put(k, v): 对新的放入的节点执行Splay
  • remove(k): 对实际被删除的节点的父节点执行Splay。删除规则同搜索二叉树

性能分析

查找，插入和删除均为O(logN)

Lab 1

3/16 上传源代码

src文件下载

1
//

Lab 2

3/20上传源代码

src文件下载

Lab 3

3/27 上传源代码

zip项目文件下载