计算机系统性能笔记

Week 4 Random Number Generation

主题：如何用计算机产生看起来像随机的数，并验证他们够不够随机

Randow Number Why & How

Why: Simulation must generate random values for variables in a specificied random distribution, such as normal, exponential distribution.

How: Tow steps:

1. Random number generation: 在[0,1]上均匀分布的随机数序列
2. Random variate generation: 将第一步生成的均匀随机数序列，转化为我们需要的分布（正态，指数）

解释：

1. 随机数 (random number)
   • 是指在 0,1] 上均匀分布的 U(0,1) 数，比如 0.12, 0.87, 0.003…
2. 随机变量样本 (random variate)
   • 是指具有某个特定分布 的样本，比如：
     • 指数分布的到达间隔时间
     • 正态分布的处理延迟
   • 它们通常是通过把 U(0,1) 随机数喂进某个变换公式得到的。

How Random Number Generators Work (递推式)

Most commonly use recurrence relation $x_n=f(x_{n−1},x_{n−2},...)$

举例：

$x_n=(5x_{n−1}+1) \bmod 16$

Seed $x_0=5$，生成的整数序列（前 32 个）：

10, 3, 0, 1, 6, 15, 12, 13, …, 4, 5, 10, 3, 0, 1, …

然后说：

$x_n$ 是在 [0,16) 之间的整数 把它们除以 16，就得到 [0,1]区间的随机数

解释：

• 随机数生成器（RNG）在计算机里通常是一个递推的数学公式：
  • 给定前一个数 $x_{n−1}$，用公式算出下一个 $x_n$。
• 上面的例子是一个最简单的线性同余生成器（LCG）特例。

知识点：

• 伪随机数生成过程是完全确定性的：
  • 给一个初始值 seed $x_0$，序列就完全确定。
• 通过 “mod” 限制范围，然后除以 m，映射到 [0,1]。

pseudo-random number的性质

• 由于f是确定的：
  • 给定seed就可以确定整个序列
• 这带来一个好处：Reproducibiliy
  • Be able to repeat a simulation experiment
• 同时要求：They pass statictical tests for randomness. No recognisable patterns

解释：

• 伪随机 (pseudo-random)：
  • 数字是由公式算出来的，但我们“希望”它们在统计上看起来像真正的随机。
• 重要优点：
  • 可以重新设定同一个 seed，复现实验条件 → 科研可复现性。

Pseudo-random vs Fully random numbers

• 为随机数产生的序列不是随机的，完全由seed决定
• 需要使用数学分析来确定是否足够接近随机
• 一些数学观点：$\pi$ , e, 非完全平方数的开方，被视作真随机数

Good Generator

• Efficiently computable
  • 仿真每次要生成几千、几万甚至更多随机数，每次计算要快
• Period should be large
  • 周期太小导致序列循环，事件模式重复
• Successive values should be
  • Correlation between successive numbers should be small(自相关小)
  • Independent
  • Uniformly distributed

解释：

判断一个 RNG 好不好，至少看三点：

1. 快：不拖累仿真速度。
2. 长周期：在整个仿真过程中不会循环。
3. 统计性质好：分布均匀，前后值不“粘连”。

Linear-Congruential Generators (LCG) & Mixed LCG

Linear-Congruential Generators

内容：

• 1951 年 Lehmer 提出：用某个数的连续幂的模剩余可以生成随机序列。
• 现代的很多随机数生成器都是这个思想的推广。

核心：

• LCG 就是：

  $x_n=(ax_{n−1}+b)\bmod m$

• 当 $b=0$ 时叫 multiplicative LCG（乘法型）； 否则叫 mixed LCG（混合型）。

Mixed Linear-Congruential Generators

内容：

• 明确写出：

  $x_n=(ax_{n−1}+b)\bmod m,a,b,m>0$

  结果：$x_n$ 在 $[0,m−1]$ 上取值。

• 优点：

  • Analysed easily
  • Certain guarantees can be made about their properties

LCG性质 - Autocorrelation

a,b,m的影响：

• period
• Autocorrelation

Properties of LCGs – Full Period 条件

内容：

• 观察：
  • 周期永远不可能超过 $m$，所以希望 $m$ 足够大。
  • $m=2^k$的实现很高效（位截断）。
• 对于 $b≠0$的情况，要想周期 = m（full period），必须满足三个条件：
  1. $m$ 和 $b$ 互质（no common factor）。
  2. 任何整除 $m$ 的素数也整除 $a−1$。
  3. 若 $m$ 是 4 的倍数，则 $a - 1$ 也是 4 的倍数。

进一步说明：满足这些条件的一种常见做法是：

• $m=2^k$
• $a=4c+1$
• $b$ 是奇数

重要性：

• 这是一套经典的full-period 条件，你不必死记，但要知道：
  • LCG 参数不是随便乱选的；
  • 选不好就会导致周期很短，随机性差。

Multiplicative LCGs

• Multiplicative LCG：$b=0$，公式变为：

  $x_n = ax_{n−1} \bmod m$

• 优点：

  • 不需要加法，理论上更高效。

• 分两类：

  1. $m=2^k$
  2. $m≠2^k$（通常取素数）

Multiplicative LCG with $m=2^k$

• 这种情况是最“硬件友好”的：mod 运算可以用位截断实现。
• 但：
  • 它的最大周期只能是 $2^{k-2}$，永远达不到 m。
• 要做到最大周期 $2^{k-2}$，需满足：
  • 乘数 $a=8i±3$
  • 初值 $x_0$ 必须是奇数

举例：

• $x_n = 5^n \bmod 2^5$
• $x_n = 7^n \bmod 2^5$

结论：

• 如果你接受“周期短一点也可以”（例如仿真时间不太长），可以用这种方式换取效率。
• 否则就用其它参数设计。

Multiplicative LCG with $m≠2^k$

内容：

• 为了避免周期过短，常选 模数为素数。
• 要想周期尽量长 $(m-1)$，要求 $a$ 是模 $m$ 的原根primitive root。

解释：

• 若 $a$ 是模 $m$ 的原根，则序列：

  $v_n = a^n \bmod m$

  会在 $1,2,…,m−1$ 中遍历所有非零剩余一次，周期 = $m−1$。

例子：

1. $x_n = 3^n \bmod 31$ → 遍历了 1 到 30 的所有数，周期 30。
2. $x_n = 5^n \bmod 31$ → 很快回到 1，周期很短（3）。

结论：

• 在乘法型 LCG 中，要获得最大周期，关键是选一个原根作为乘数。

Randomness Test（随机性检验类型）

Goal: To ensure that the random number geterator produces a random stream.

常见方法：

• Goodness of Fit Tests：卡方检验 (Chi-square)、t-test（更多用于均值比较）
• Autocorrelation：检查前后值是否相关
• 具体名字：
  • Ljung–Box test（对多个滞后阶的整体自相关检验）
  • Durbin–Watson test（主要对一阶自相关）
  • Wald–Wolfowitz runs test（游程检验：看 0/1 序列中切换频率是否合理）

大意：

• 好的 RNG 必须通过一系列统计检验，才能称得上“随机性良好”。

Week 5 Queuing Moding

Components of Model (模型组成)

1. Input Source
2. Queuing Discipline(排队规则)
   • FIFO
   • Priority
   • LIFO, Random
3. Service Mechanism(服务机制)
   • One or more servers

现实的排队案例

System	Arrival Process	Service Process
Bank	Customers arrive	Tellers serve customers
Pizza Parlor	Orders phoned in	Orders delivered
Blood Bank	Pints donated	Patients use blood
Shipyard	Ships arrive for repair	Ships repaired & return
Printers	Jobs arrive	Documents printed

Typical Performance Questions

排队模型要回答：

• 平均系统人数 L
• 平均逗留时间 W
• 队列长度 Lq
• 等待时间 Wq
• 服务器空闲概率
• 客户拒绝概率（系统满了）

这些都是运维、系统设计、网络分析中常见指标。

常见的队列结构

• 一排多服
• 多排多服

符号定义

$N(t)$：t 时刻系统人数

$P_k(t)$：t 时刻人数为 k 的概率

s：服务器数量

$λ_k$：当系统里有 k 个顾客时的到达率

• 当系统里当前k个顾客时，下一次顾客到达发生的平均速率
• 在这个状态下，每单位时间平均有 $λ_k$ 个顾客会到来

$µ_k$：服务率（k 个服务中的退出率）

• 当系统里有k个顾客时，每单位时间平均会有 $µ_k$ 个离开的顾客

如果到达率与人数无关：

$λ_k = λ$（Poisson 到达的典型假设）

服务率：

• 当 k < s（顾客闭服务器少），$µ_k$ = $kµ$（并行服务）
• 当 k ≥ s，$µ_k$ = $sµ$

利用率（最重要指标）

$\rho = \frac{\lambda}{s\mu}$

必须 ρ < 1，否则队列发散（不稳定）

Details

• λ：总体平均到达率
  • 单位：顾客/任务 每单位时间
  • 例：每小时来 5 个顾客 → λ = 5 / hour
• μ：单个服务器的平均服务率
  • 单位：顾客/任务 每单位时间
  • 例：一个服务员平均每小时服务 2 个顾客 → μ = 2 / hour
• s：服务器数量（并行服务个数）
  • 例：3 个窗口 → s = 3

那么：

• 总的 服务能力上限（所有服务器一起干活的最大吞吐）就是：$sμ$

  单位：顾客/小时

于是有：

$\rho = \frac{\text{到达能力}}{\text{服务能力上限}} = \frac{\lambda}{s\mu}$

所以从 直观上看：

ρ 就是“负载占容量的比例”。

• ρ = 0.5 → 系统平均上只用了一半的处理能力
• ρ 接近 1 → 系统基本满负荷运行
• ρ > 1 → 需求比能力大，系统会一直“积压”任务

稳态符号

• $π_k$：系统恰好有 k 人的概率，整个队列系统的计算基础

• L：系统中平均人数（包括服务中与等待)
  • $L = \sum_{k=0}^{\infty} k \pi_k$
• $L_q$：平均排队人数(只算等待)
  • $L_q = \sum_{k=s+1}^{\infty} (k-s)\pi_k$
  • （k-s)人在排队,一共k人，s人被服务
• $L_S$: 平均正在服务的人
  • $L_S = L - L_q$
• $\bar{\lambda}$：有效到达率
• 随着队列不断增长(系统容量K），到达者可能被拒绝
  • 这时实际进入系统的平均到达率比$\lambda$小
• W：平均系统时间(包括等待和服务时间)
  • Little’s Law：$W = \frac{L}{\bar{\lambda}}$
• $W_q$：平均排队时间(不包括服务时间)
  • Little’s Law：$W_q = \frac{L_q}{\bar{\lambda}}$
• $E$：服务器效率
  • $E = \frac{L_s}{s}$

Little’s Law

$L=λW,Lq=λW_q$

If $µ_k = µ$ for all $k \geq 1$ then $W = W_q + \frac{1}{µ}$

等待时间 2 小时，到达率每小时 3 人 → L = 6 人。

Little 定律是所有排队系统的基础。

Brith and Death Processes

假设：

• 到达间隔 ~ Exponential($λ_k$)
• 服务时间 ~ Exponential($µ_k$)
• 相互独立（memoryless 性质）

系统状态 N(t) 表示系统人数。

队列九讲（3 服务器系统）

系统参数：

• 到达率(进入速度)：λ = 5
• 服务率(离开速度)：µ = 2
• 服务器数 s = 3
• 系统容量 K = 6（超过 6 会 balk）

1. 计算 $λ_k$ and $µ_k$：

到达率 λₖ：

• 当系统未满时（k < 6）

  $\lambda_k = \lambda = 5$

• 当系统满时（k = 6）

  $\lambda_6 = 0$

服务率 μₖ：

• 若 k < s（k < 3）

  $\mu_k = k\mu = 2k$

• 若 k ≥ s

  $u_k = s\mu = 6$

2. 求 πₖ 的通式

平衡方程：

$\lambda_{k-1}\pi_{k-1} = \mu_k\pi_k$

逐次递推：

$\pi_k = \frac{\lambda_{k-1}}{\mu_k}\pi_{k-1}$

最终得到：

$\pi_k = C_k \pi_0$

然后通过归一化：

$\sum_{k=0}^6 \pi_k = 1$

得到 π₀、π₁、…、π₆

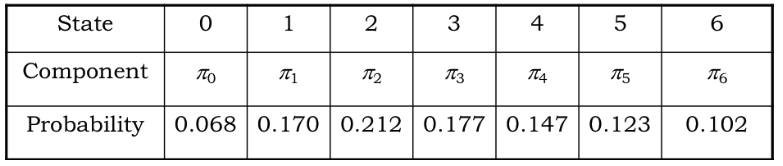
问题一：What is the probability that all servers are idle?

服务器全部空闲

全部空闲 ↔ 系统中 0 人

$\Pr(\text{all idle}) = \pi_0 = 0.068$

问题二：What is the probability that a customer will not have to wait?

顾客无需等待的概率 -> 到达时系统人数k < s

即 k = 0, 1, 2

$\Pr(\text{no wait}) = \pi_0 + \pi_1 + \pi_2$

问题三：What is the probability that a customer will have to wait?

顾客必须等待的概率

$\Pr(\text{wait}) = 1 - \Pr(\text{no wait}) = 0.55$

问题四：What is the probability that a customer balks?

顾客被拒绝的概率

拒绝发生在系统满时：

$\Pr(\text{balk}) = \pi_6 = 0.102$

问题五：Expected number in queue 队列人数：

排队人数 = k − 3（当 k ≥ 4）

$L_q = 1\pi_4 + 2\pi_5 + 3\pi_6 = 0.700$

问题六：Expected number in service 服务中人数：

$L_s = 0π0+1π1+2π2+3π3+3π4+3π5+3π6 = 2.244$

问题七：Expected number in the system 系统人数：

$L = L_q + L_s = 2.944$

问题八：Efficiency of the servers 服务器效率：

$E = \frac{L_s}{s} = \frac{2.244}{3} = 0.748$

问题九：计算等待时间 Ws,Wq,W

1. 先算有效到达率λ̄

因为满时到达被拒绝：

$\bar{\lambda} = \sum_{k=0}^6 \lambda_k \pi_k$

已知 λₖ = 5（k < 6），λ₆=0：

$\bar{\lambda} = 5(1 - π_6)=5(1−0.102)=4.488/hour$

2. 平均等待时间：

• 服务时间：$W_s = L_s / λ̄ = 1/ u= 0.5 小时$
• 等待时间：$W_q = L_q / λ̄ = 0.156 小时$
• 总时间：$W = L / λ̄ = 0.656 小时$

Week 6 M/M/1 Queuing Model

M/M/1：单服务器排队

M/M/c：c 个服务器并行服务

M/M/1

M/M/1	Arrival	Service	Servers
M	Markovian（泊松到达）	Markovian（指数分布）	1 个服务器

Brith-death结构：

• λₖ = λ（与人数无关）

• μₖ = μ（单服务器服务率，人数 ≥1 时服务速率固定 μ）

ρ = λ / μ 利用率：进入/离开

稳态概率推导

1. 生灭平衡方程：

$\lambda \pi_{k-1} = \mu \pi_k \quad\Rightarrow\quad \pi_k = \rho \pi_{k-1}$

迭代得到：

$\pi_k = \rho^k \pi_0$

2. 用归一化求 π₀

$\sum_{k=0}^{\infty} \pi_k = \sum_{k=0}^{\infty} \rho^k \pi_0 = \pi_0 \frac{1}{1 - \rho} = 1 \Rightarrow \pi_0 = 1 - \rho$

3. 结论

$π_0 = 1 - ρ, π_k=(1−ρ)ρ^k$

性能指标

1. 平均系统人数

   定义：$L = \sum_{k=0}^{\infty} k\pi_k = \sum_{k=0}^{\infty} k (1-\rho)\rho^k$

   这是几何分布 $\text{Geom}(1-\rho)$的期望：

   $E[k] = \frac{\rho}{1-\rho}$

   于是：

   $L = \frac{\rho}{1-\rho} = \frac{\frac{\lambda}{\mu}}{1-\frac{\lambda}{\mu}} = \frac{\lambda}{\mu - \lambda}$

2. 平均排队人数

   定义：排队人数 = 系统人数 - 服务人数

   $L_q = L - (1 - \pi_0) = \frac{\rho}{1 - \rho} - \rho = \frac{\lambda}{\mu - \lambda} - \frac{\lambda}{\mu} =\frac{λ^2}{μ(μ−λ)}$

3. Little’s Law

   $L=λW,Lq=λWq$

4. 平均等待时间

   $W=\frac{1}{μ−λ}$

   $W_q = \frac{λ}{μ(μ−λ)}$

例题：网络网关

已知

• 单网关（单服务器）

• 到达速率：$\lambda = 125$ packets/s

• 服务时间：$W_s = 2$ ms

先求一些值

问题1

• What is the probability of buffer overflow if the gateway had only 13 buffers?

等待区只有13个位置，数据溢出的概率

$\mu = 1/W_s = 500$ 服务的速度

$\rho = \frac{\lambda}{\mu} = 0.25$

$Pr(k >= 14) = \sum_{k=14}^{\infty} \pi_k = \sum_{k=14}^{\infty}(1-\rho)\rho^k$

接近0，所以基本不会丢包

问题2

• How many buffers do we need to keep packet loss below one packet per million?

要保证丢包率小于1 ppm

• $Pr(k >= B) < 10^{-6}$
• 求B

例题：M/M/1/2 维修系统

场景：

• 两台机器，一坏就修
• 修理工一次只能修一台
• 状态 = “坏掉的机器数量”

已知

• 机器平均10h坏一次 -> 坏的速率 $\lambda = 1/10 hr$
• 修理时间，平均8小时修一台 -> $\mu = 1/8 hr$
• 两台机器可能同时坏

状态 k	含义	λₖ	μₖ
0	两台都好	λ₀ = 2λ	μ₀ = 0
1	一坏	λ₁ = 1λ	μ₁ = μ
2	两坏	λ₂ = 0	μ₂ = μ

问题

• 求 $\pi_k$
• 计算 $L, L_q, W, W_q$
• 修理工忙的比例
• 各个机器的工作占比

1. 建立稳态 ---- 求 $\pi_k$

   $\lambda_0\pi_0 = \mu_1\pi_1$

   $\lambda_1\pi_1 = \mu_2\pi_2$

   $\pi_0 + \pi_1 + \pi_2 = 1$

   推导可得

   $\pi_0 + \frac{\lambda_0\pi_0}{\mu_1} + \frac{\lambda_0\lambda_1\pi_0}{\mu_1\mu_2} = 1$

   这样就可以求出$\pi_0, \pi_1, \pi2$

2. 计算性能指标

系统平均坏机数:

$L = 0\pi_0 + 1\pi_1 + 2\pi_2$

修理工忙碌概率(服务器)

$Pr(忙) = \pi_1 + \pi_2$

1号机器工作的概率

$pr = \pi_0 + \frac{1}{2}\pi_1$

M/M/s

M./M/s: Poisson 到达 + 指数服务 + s个服务器

• 到达过程: Poisson, 速率$\lambda$
• 服务率: $\mu$
• 服务器数: $s$
• 稳定条件： $\lambda < s\mu$

状态 n = 系统中顾客总数（排队+服务）

到达率：λₙ = λ（还没涉及有限容量，所以不看 n）

服务率 μₙ 随 n 变化（关键）：

• 当 1 ≤ n ≤ s：最多同时服务 n 人

  $\mu_n = n\mu$

• 当 n ≥ s：所有 s 个服务器都忙，服务率封顶

  $\mu_n = s\mu$

例题：电话客服排队

场景

• 呼叫到达率速度 $\lambda = 10$ 通/分钟
• 平均服务时间1分钟 -> $\mu = 1$
• 有s个客服

问题：需要多少个客服才能稳定

$\rho = \frac{\lambda}{s\mu} = \frac{10}{s \times 1} < 1$

所以 $s > 10$

M/M/1/K & M/M/2/5

在排队空间有限的情况下

例题：加工站 + 有限排队空间

已知

• 到达率 $\lambda = 1.5$
• 服务时间 $W_s = 0.5$ min -> $\mu = 2$ 件/分钟
• 队伍最多3个等待

问题

1. 全部超过5%的零件被balk的概率
2. 被直接服务的零件中，等待时间>1 min的比例 <= 10%

重新定义已知

• s = 1（一个机器/服务器）

• 最大系统容量 K = 4

为什么是 4？ 1 个在服务 + 最多 3 个排队 ⇒ 系统里最多 4 个零件

• 调用源大小 N = ∞（无限顾客源）

• λ = 1.5/min，μ = 2/min

• 利用率：

$\rho = \frac{\lambda}{\mu} = \frac{1.5}{2} = 0.75$

1. 求$\pi_k$ —可直接根据下方公式

2. Balking probability $P_F$

   $P_F = \pi_4 = 0.104 = 10.4\%$

3. 平均有效到达率 $\bar{\lambda} = \lambda(1- P_F)$: 被挡在门外的部分不算真正进入系统

4. 系统平均人数: $L = \sum k\pi_k$

5. 平均在系统中的时间: 用little 公式 $W = \frac{L}{\lambda}$

6. 服务器效率： $E = \rho(1-P_F)$

7. 等待时间超过1min的概率：

   $Pr(T_q > 1)$ 这个推导有点难，省略了

例题：增加一个服务器 M/M/2/5

将系统改造为两个服务器

• s = 2
• K =5 （2个服务3个排队)

计算方法类似

队列调度规则

• FIFO
• LIFO：后进先出
• Processor sharing：时间片轮转
• Priority
• Shortest job first
• Shortest remaining processing time

服务设施架构

• 单服务器
• 多服务器
• 串联系统

顾客行为

• Balking: 看到队伍太长，直接不排队
• Jockeying: 在多队列系统中，来回换队
• Reneging：排了一会不耐烦离开

Week 13 Revision

总览

Web 服务器性能评估情景：评估类似生产负载的新 Web 服务器 目标：确定它是否满足 200ms 的平均响应时间要求

1. 评价方法
   • Analytical
   • Simulation
   • Measurement
2. 评估指标
   • 衡量系统好坏的标志
3. 工作负载生成
   • 系统评估的前提是有输入负载，要么真实trace，要么随机生成
4. 排队论
   • 核心数学模型，用来估计延迟、等待时间、吞吐
5. 马尔可夫模型
   • 排队论内部数学基础
6. 统计分析
   • 仿真和测量都不是精确值，所以要用统计学

评估方法选择

• Analytical: 快但是简化严重
• Simulation: 较真实但要写代码
• Measurement: 最真实但代价高

大多数性能研究采用 Hybrid Approach：

1. 用 M/M/1 衡量是否可行（解析模型）
2. 用仿真进行细节验证
3. 用真实测量做最终确认

指标 + 工作负载生成

指标（Metrics）告诉你要测什么，Workload 告诉你怎么测。

排队论

马尔卡夫模型和稳态分析

统计分析

1. Sample Vs Population
   • 仿真只能取样，但目标是估计真实系统行为
2. Confidence Interval
3. Central Limit Theorem
4. QQ Plot
   • 用于判断样本分布是否符合理论分布
5. Clustering
   • 用于workload分析，分类用户请求模式

结果 & 验证